[:ru]Актуальность проекта: Исследования по построению и усовершенствованию разностных схем, по доказательству устойчивости и изучению сходимости решения ведутся в крупных научных центрах и высших учебных заведениях мира (в частности США, Великобритания, Германия, Франция, Италия, Норвегия, Нидерланды, Испания, Россия).
В результате современных проведенных научных исследований в мире для вычисления разрывных решений квазилинейных систем уравнений по построению разностных схем, доказательству их сходимости получен целый ряд нетрадиционных научных результатов: обоснован метод “замороженных коэффициентов” для разностных схем, развит энергетический метод исследования устойчивости Институт вычислительной математики Российской академии наук (ИВМ РАН); с учетом критерия монотонности разработан алгоритм построения нелинейных, монотонных схем высокого порядка аппроксимации для уравнений и систем гиперболического типа, основанный на использовании метода неопределенных коэффициентов (Институт автоматизации проектирования РАН); для гиперболических систем с постоянными коэффициентами на движущейся области, применяя энергетический метод, получена априорная оценка для решения смешанной задачи; после соответствующей замены переменных получена гиперболическая система уравнений с переменными коэффициентами. С помощью операторов суммирования по частям (Summation-by-Parts) по пространственным координатам получена устойчивая разностная схема. (Швеция, Linköping University); создана теория для однородных краевых задач с постоянными и переменными коэффициентами, построена строгая теория устойчивости для определенных краевых задач (Adelphy College, Garden City, Brookhaven National laboratories, Upton, Нью-Йорк, США; University of Uppsala, Швеция); исследованы корректности прямых и обратных задач для одномерных нелинейных уравнений гиперболического типа (Logo Alpen Adria Universität); для построения устойчивых решений смешанной задачи двумерной линейной гиперболической системы (в случае переменных коэффициентов и с младшими членами) создана функция Ляпунова, и получена априорная оценка для неё (University Pierre et Marie Curie, Париж, Universitè catholique Louvain, Louvain-La-Neuve, Бельгия); построены консервативные разностные схемы для параболических и гиперболических уравнений и систем уравнений, для которых выполнен аналог этого закона (Fudan University, Shanghai, Китай); для нелинейных гиперболических систем, представляемых в специальном виде, построена адекватная вычислительная модель, в которой доказательство теоремы об устойчивости разносных схем основывается на построении дискретного интеграла энергии (Институт математики Сибирского отделения Российской академии наук; Национальный университет Узбекистана).
На сегодня в мире широко осуществляются научно-исследовательские работы в приоритетных направлениях, в том числе: разработка методов приближенного решения смешанных задач на линейных двумерных и более-мерных гиперболических системах с переменными коэффициентами; исследование устойчивость вычислительных методов для численного решения смешанных задач для квазилинейных гиперболических систем.
Устойчивость как основное свойство разностных схем, является самостоятельной областью исследования. В настоящее время для линейных задач математической физики достаточно полно разработана теория разностных схем. Монотонные разностные схемы играют важную роль при численном решении систем уравнений гиперболического типа.
До сегодняшнего дня ещё не рассматривался вопрос разработки численного метода, с помощью которого можно провести численный расчет смешанной задачи граничного управления гиперболическими системами. Это и есть основная задача настоящего проекта. Учет управления достигается с помощью введения функции управления в граничных условиях, т.е., так называемым способом граничного управления устойчивости. Все вышеперечисленное обуславливает актуальность проекта.
Цель проекта: Целью проекта является разработка численных методов, с помощью которых можно провести численный расчет смешанной задачи граничного управления симметрической t-гиперболической системой с диссипативными граничными условиями. Это достигается с помощью введения функции управления в граничных условиях, т.е так называемым способом граничного управления.

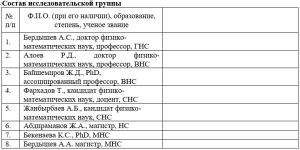
Опубликованы статьи в журналах (Список публикации)
- Berdyshev A, Aloev R, Abdiramanov Z, Ovlayeva M. An Explicit–Implicit Upwind Difference Splitting Scheme in Directions for a Mixed Boundary Control Problem for a Two-Dimensional Symmetric t-Hyperbolic System / Symmetry 2023, 15, (10):1863. (WoS: CiteScore — Q1 (General Mathematics); Scopus – 93) https://doi.org/10.3390/sym15101863
- Abdiramanov Zh., Berdyshev A., Aloev R. Investigation of the exponential stability of a numerical solution of a mixed problem for the shallow water equation. 5th International Conference on Problems of Cybernetics and Informatics (PCI 2023). Abstracts, pp. 119-120. Baku, Azerbaidzhan.
- Абдираманов Ж., Бердышев А. Устойчивость численного решения разностной задачи для уравнения Сен-Венана. Тезисы докладов VII Всемирного Конгресса математиков тюркского мира (TWMS Congress-2023). с. 457. 20-23 сентября 2023 г. Туркестан, Казахстан.
Сделаны выступления на следующих международных научных форумах:
— Международной конференции “5th International Conference on Problems of Cybernetics and Informatics (PCI 2023)”. 28–30 августа 2023 г. г. Баку, Азербайджан;
— VII Всемирном Конгрессе математиков тюркского мира (TWMS Congress-2023). 20-23 сентября 2023 г. Туркестан, Казахстан.[:en]The relevance of the project: Research on the construction and improvement of difference schemes, on proving stability and studying the convergence of solutions is carried out in large scientific centers and higher educational institutions of the world (in particular the USA, Great Britain, Germany, France, Italy, Norway, the Netherlands, Spain, Russia).
As a result of modern scientific research conducted in the world to calculate discontinuous solutions of quasi-linear systems of equations for the construction of difference schemes, to prove their convergence, a number of unconventional scientific results have been obtained: the method of “frozen coefficients” for difference schemes has been substantiated, the energy method of stability research has been developed by the Institute of Computational Mathematics of the Russian Academy of Sciences (IVM RAS); taking into account the monotony criterion, an algorithm for constructing nonlinear, monotonic high-order approximation schemes for equations and systems of hyperbolic type based on the use of the method of indefinite coefficients (Institute of Design Automation of the Russian Academy of Sciences) has been developed; for hyperbolic systems with constant coefficients on a moving area, using the energy method, an a priori estimate for solving a mixed problem has been obtained; after appropriate replacement of variables A hyperbolic system of equations with variable coefficients is obtained. Using the Summation-by-Parts operators for spatial coordinates, a stable difference scheme is obtained. (Sweden, Linköping University); a theory for homogeneous boundary value problems with constant and variable coefficients was created, a rigorous stability theory for certain boundary value problems was built (Adelphy College, Garden City, Brookhaven National Laboratories, Upton, New York, USA; University of Uppsala, Sweden); the correctness of direct and inverse problems for one-dimensional nonlinear hyperbolic equations (Logo Alpen Adria Universität); to construct stable solutions to the mixed problem of a two-dimensional linear hyperbolic system (in the case of variable coefficients and with minor terms), the Lyapunov function was created, and an a priori estimate for it was obtained (University Pierre et Marie Curie, Paris, Universitè catholique Louvain, Louvain-La-Neuve, Belgium); conservative difference schemes for parabolic and hyperbolic equations and systems of equations for which an analogue of this law is performed (Fudan University, Shanghai, China); for nonlinear hyperbolic systems presented in a special form, an adequate computational model has been constructed in which the proof of the stability theorem of disparate circuits is based on the construction of a discrete energy integral (Institute of Mathematics of the Siberian Branch of the Russian Academy of Sciences; National University of Uzbekistan).
Today, scientific research is widely carried out in the world in priority areas, including: the development of methods for approximate solution of mixed problems on linear two-dimensional and higher-dimensional hyperbolic systems with variable coefficients; the study of the stability of computational methods for the numerical solution of mixed problems for quasi-linear hyperbolic systems.
Stability, as the main property of difference schemes, is an independent field of research. Currently, the theory of difference schemes has been developed quite fully for linear problems of mathematical physics. Monotone difference schemes play an important role in the numerical solution of systems of hyperbolic equations.
To date, the issue of developing a numerical method by which a numerical calculation of the mixed problem of boundary control of hyperbolic systems can be carried out has not yet been considered. This is the main task of this project. Control accounting is achieved by introducing a control function in boundary conditions, i.e., the so-called boundary stability control method. All of the above determines the relevance of the project.
Project objective: The aim of the project is to develop numerical methods that can be used to numerically calculate the mixed boundary control problem of a symmetric t-hyperbolic system with dissipative boundary conditions. This is achieved by introducing a control function in boundary conditions, i.e. the so-called boundary control method.
…
Articles have been published in journals (List of publications)
Berdyshev A, Aloev R, Abdiramanov Z, Ovlayeva M. An Explicit–Implicit Upwind Difference Splitting Scheme in Directions for a Mixed Boundary Control Problem for a Two-Dimensional Symmetric t-Hyperbolic System / Symmetry 2023, 15, (10):1863. (WoS: CiteScore — Q1 (General Mathematics); Scopus – 93) https://doi.org/10.3390/sym15101863
Abdiramanov Zh., Berdyshev A., Aloev R. Investigation of the exponential stability of a numerical solution of a mixed problem for the shallow water equation. 5th International Conference on Problems of Cybernetics and Informatics (PCI 2023). Abstracts, pp. 119-120. Baku, Azerbaidzhan.
Abdiramanov J., Berdyshev A. Stability of the numerical solution of the difference problem for the Saint-Venant equation. Abstracts of the VII World Congress of Mathematicians of the Turkic World (TWMS Congress-2023). pp. 457. September 20-23, 2023 Turkestan, Kazakhstan.
Presentations have been made at the following international scientific forums:
— International Conference “5th International Conference on Problems of Cybernetics and Informatics (PCI 2023)». August 28-30, 2023, Baku, Azerbaijan;
— The VII World Congress of Mathematicians of the Turkic World (TWMS Congress-2023). September 20-23, 2023 Turkestan, Kazakhstan.[:kk]Жоба өзектілігі. Айырым сұлбаларын құру және жетілдіру, орнықтылықты дәлелдеу және шешімнің жинақтылығын зерттеу бойынша зерттеулер әлемнің ірі ғылыми орталықтары мен жоғары оқу орындарында (атап айтқанда АҚШ, Ұлыбритания, Германия, Франция, Италия, Норвегия, Нидерланды, Испания, Ресей) жүргізілуде.
Әлемде жүргізілген заманауи ғылыми зерттеулердің нәтижесінде айырымдық сұлбаларын құру бойынша квазисызықтық теңдеулер жүйесінің үзіліссіз шешімдерін есептеу, олардың жинақтылығын дәлелдеу үшін бірқатар дәстүрлі емес ғылыми нәтижелер алынды: айырымдық сұлбалар үшін «мұздатылған коэффициенттер» әдісі негізделді, орнықтылықты зерттеудің энергетикалық әдісі дамытылды Ресей Ғылым академиясының Есептеу математикасы институты (РҒА ИВМ); монотондылық критерийін ескере отырып, анықталмаған коэффициенттер әдісін қолдануға негізделген гиперболалық типтегі теңдеулер мен жүйелерге жуықтаудың жоғары ретті сызықтық емес, монотонды сұлбаларын құру алгоритмі жасалды (РҒА жобалауды автоматтандыру институты); қозғалмалы аймақта тұрақты коэффициенттері бар гиперболалық жүйелер үшін энергетикалық әдісті қолдана отырып, аралас есепті шешу үшін априорлық бағалау алынады; айнымалыларды тиісті алмастырудан кейін айнымалы коэффициенттері бар гиперболалық теңдеулер жүйесі алынды. Бөліктеп қосындылау операторларының көмегімен (Summation-by-Parts) кеңістіктік координаттар бойынша тұрақты айырымдық сұлбасы алынды. (Швеция, Linköping University); тұрақты және айнымалы коэффициенттері бар біртекті шеттік есептер үшін теория құрылды, белгілі бір шеттік есептер үшін қатаң тұрақтылық теориясы құрылды (Adelphy College, Garden City, Brookhaven National laboratories, Upton, Нью-Йорк, АҚШ; University of Uppsala, Швеция); гиперболалық типтегі бір өлшемді сызықты емес теңдеулер үшін тікелей және кері есептердің қисындылығы зерттелді (Logo Alpen Adria Universität); екі өлшемді сызықтық гиперболалық жүйенің аралас есебінің орнықты шешімдерін құру үшін (айнымалы коэффициенттер жағдайында және кіші мүшелермен) Ляпунов функциясы құрылды және ол үшін априорлық баға алынды (University Pierre et Marie Curie, Париж, Universitè catholique Louvain, Louvain-la-Neuve, Бельгия); осы Заңның аналогы орындалатын параболалық және гиперболалық теңдеулер мен теңдеулер жүйелері үшін консервативті айырымдық сұлбалары салынды (Фудан университеті, Шанхай, Қытай); арнайы түрде ұсынылған сызықтық емес гиперболалық жүйелер үшін адекватты есептеу моделі құрылды, онда әртүрлі схемалардың орнықтылығы туралы теореманың дәлелі энергияның дискретті интегралын құруға негізделген (Ресей Ғылым академиясының Сібір филиалының математика институты; Өзбекстан Ұлттық университеті).
Бүгінгі таңда әлемде басым бағыттарда ғылыми-зерттеу жұмыстары кеңінен жүзеге асырылуда, оның ішінде: айнымалы коэффициенттері бар сызықтық екі өлшемді және одан да көп өлшемді гиперболалық жүйелерде аралас есептерді жуықтап шешу әдістерін әзірлеу; квазисызықты гиперболалық жүйелер үшін аралас есептерді сандық шешуге арналған есептеу әдістерінің орнықтылығын зерттеу.
Айырымдық схемаларының негізгі қасиеті ретінде өзіндік тәуелсіз зерттеу саласы болып табылады. Қазіргі уақытта Математикалық физиканың сызықтық есептері үшін айырымдық сұлбаларының теориясы жеткілікті түрде дамыған. Монотонды айырымдық сұлбалары гиперболалық типтегі теңдеулер жүйесін сандық шешуде маңызды рөл атқарады.
Бүгінгі күнге дейін гиперболалық жүйелерді шекаралық басқарудың аралас мәселесін сандық есептеуге болатын сандық әдісті әзірлеу мәселесі әлі қарастырылмаған. Бұл-осы жобаның негізгі міндеті. Басқару есебіне шекаралық жағдайларда басқару функциясын енгізу арқылы қол жеткізіледі, яғни орнықтылықты шекаралық басқару әдісі деп аталады. Жоғарыда айтылғандардың барлығы жобаның өзектілігін анықтайды.
Жоба мақсаты. Жобаның мақсаты-диссипативті шекаралық шарттары бар симметриялық t-гиперболалық жүйені шекаралық басқарудың аралас мәселесін сандық есептеуге болатын сандық әдістерді әзірлеу. Бұған шекаралық жағдайларда басқару функциясын енгізу арқылы қол жеткізіледі, яғни шекаралық басқару әдісі деп аталады.
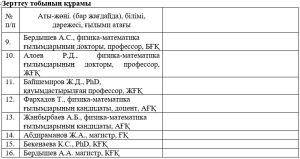
Журналдарда жарияланған мақалалар (Жарияланымдар тізімі)
- Berdyshev A, Aloev R, Abdiramanov Z, Ovlayeva M. An Explicit–Implicit Upwind Difference Splitting Scheme in Directions for a Mixed Boundary Control Problem for a Two-Dimensional Symmetric t-Hyperbolic System / Symmetry 2023, 15, (10):1863. (WoS: CiteScore — Q1 (General Mathematics); Scopus – 93) https://doi.org/10.3390/sym15101863
- Abdiramanov Zh., Berdyshev A., Aloev R. Investigation of the exponential stability of a numerical solution of a mixed problem for the shallow water equation. 5th International Conference on Problems of Cybernetics and Informatics (PCI 2023). Abstracts, pp. 119-120. Baku, Azerbaidzhan.
- Абдираманов Ж., Бердышев А. Устойчивость численного решения разностной задачи для уравнения Сен-Венана. Тезисы докладов VII Всемирного Конгресса математиков тюркского мира (TWMS Congress-2023). с. 457. 20-23 сентября 2023 г. Туркестан, Казахстан.
Келесі халықаралық ғылыми форумдарда баяндамалар жасалды:
— «5th International Conference on Problems of Cybernetics and Informatics (PCI 2023)»халықаралық конференциясы. 2023 жылғы 28-30 тамыз Баку, Әзірбайжан;
— Түркі әлемі математиктерінің VII Дүниежүзілік Конгресі (TWMS Congress-2023). 2023 жылғы 20-23 қыркүйек Түркістан, Қазақстан.
[:]






